Diagrama de Venn

Te explicamos qué es un diagrama de Venn, para qué sirve y sus elementos. Además, te contamos qué tipos existen y cómo hacerlos.

¿Qué es un diagrama de Venn?

El diagrama de Venn es un tipo de organizador gráfico que muestra cómo se relacionan dos o más conjuntos de elementos, puesto que, mediante círculos superpuestos, representa qué características comparten y cuáles no dos o más categorías, grupos, ideas, conceptos, teorías, entre otros.

En el diagrama de Venn hay:

• Un rectángulo. Representa el universo, es decir, la totalidad de elementos, y se designa con un título. En algunos diagramas no hay un rectángulo, pero sí un título.
• Dos o más círculos. Representan los conjuntos, las ideas, los conceptos o las categorías que se designan con un título o una oración.
• Palabras o frases. Representan los elementos de un conjunto, los integrantes de una categoría o una serie de características.
• Una superposición entre los círculos. Representa los vínculos entre los conjuntos, que pueden ser de intersección, inclusión o disyunción.

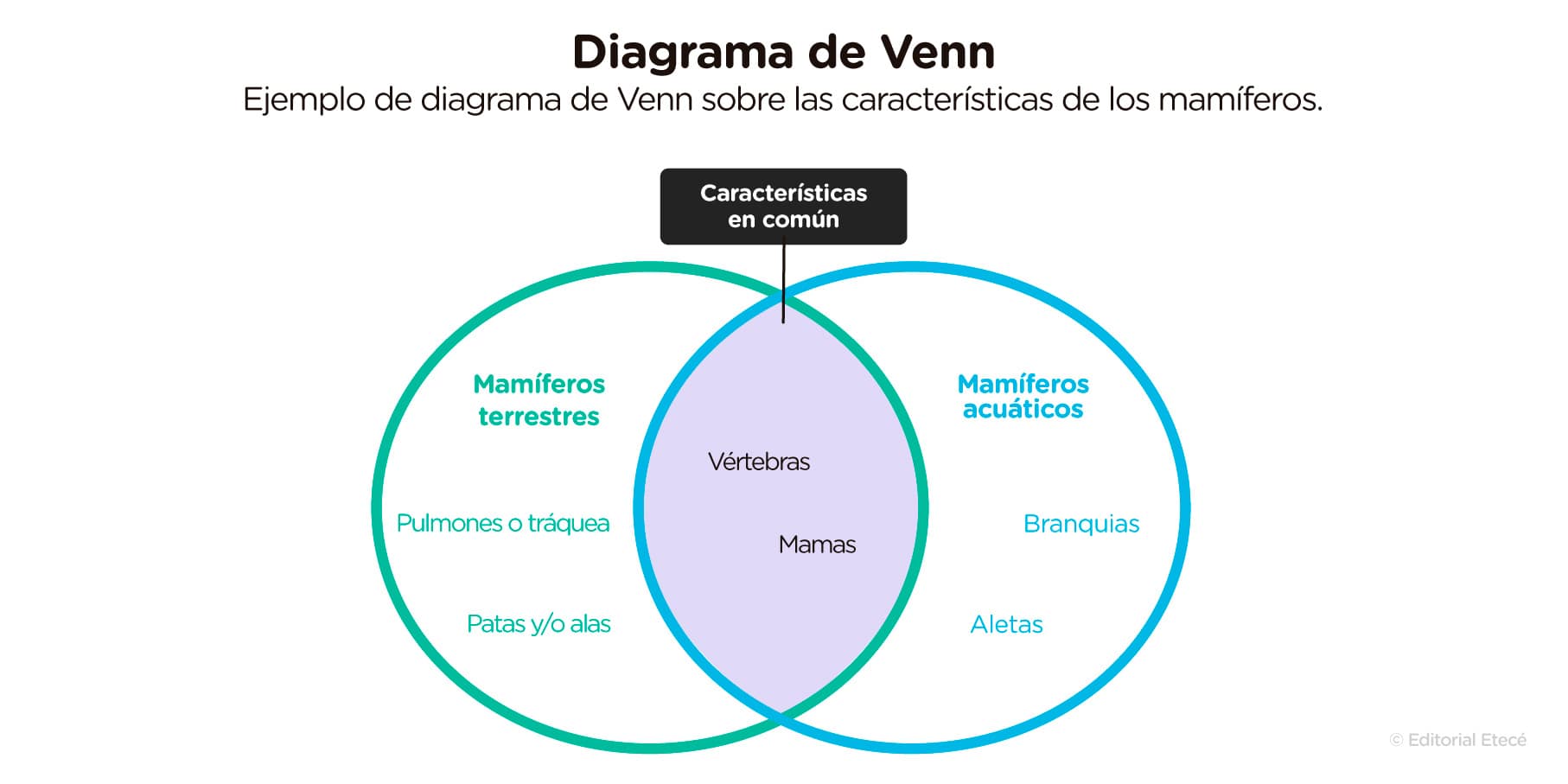
Por ejemplo, en un diagrama sobre los mamíferos, el universo es características de los mamíferos y hay dos conjuntos: mamíferos terrestres y mamíferos acuáticos. En cada círculo, se escriben las características que comparten los miembros de cada clase y en la superposición de ambos círculos, se anotan las características en común de ambos conjuntos.

Puede servirte: Diagrama

Características del diagrama de Venn

A diferencia de la mayoría de los organizadores gráficos, el diagrama de Venn permite:

• Identificar qué y cuántos conjuntos hay en relación con un tema.
• Mostrar qué vínculo hay entre los conjuntos.
• Indicar a qué conjunto pertenece cada elemento y, en algunos casos, identificar elementos que forman parte de dos o más conjuntos.
• Determinar que puede haber elementos que no pertenecen a ningún conjunto.

¿Para qué sirve el diagrama de Venn?

El diagrama de Venn presenta grandes ventajas y se emplea con distintos fines:

• Muestra información visualmente. Ayuda a organizar la información para que sea más fácil de comprender.
• Permite graficar la relación entre dos o más conjuntos. Sirve para ver qué características o qué elementos tienen en común dos o más conjuntos y cuáles son sus diferencias.
• Es útil para hacer clasificaciones. Sirve para determinar qué elementos pertenecen a cada categoría.
• Permite hacer comparaciones. Sirve para contrastar las características o los elementos de objetos, productos, lugares, teorías, entre otros.
• Es una herramienta para tomar decisiones. Permite ver con más claridad dos o más opciones y reflexionar sobre cuál es la más conveniente.

Tipos de diagrama de Venn

Existen distintos tipos de diagramas de Venn, según el tipo de relación que se establece entre los conjuntos:

Diagrama de Venn de intersección

Muestra que hay elementos que pertenecen a uno u otro conjunto y elementos que pertenecen a ambos. Puede haber dos o más círculos, según cuántos conjuntos sean. Por ejemplo:

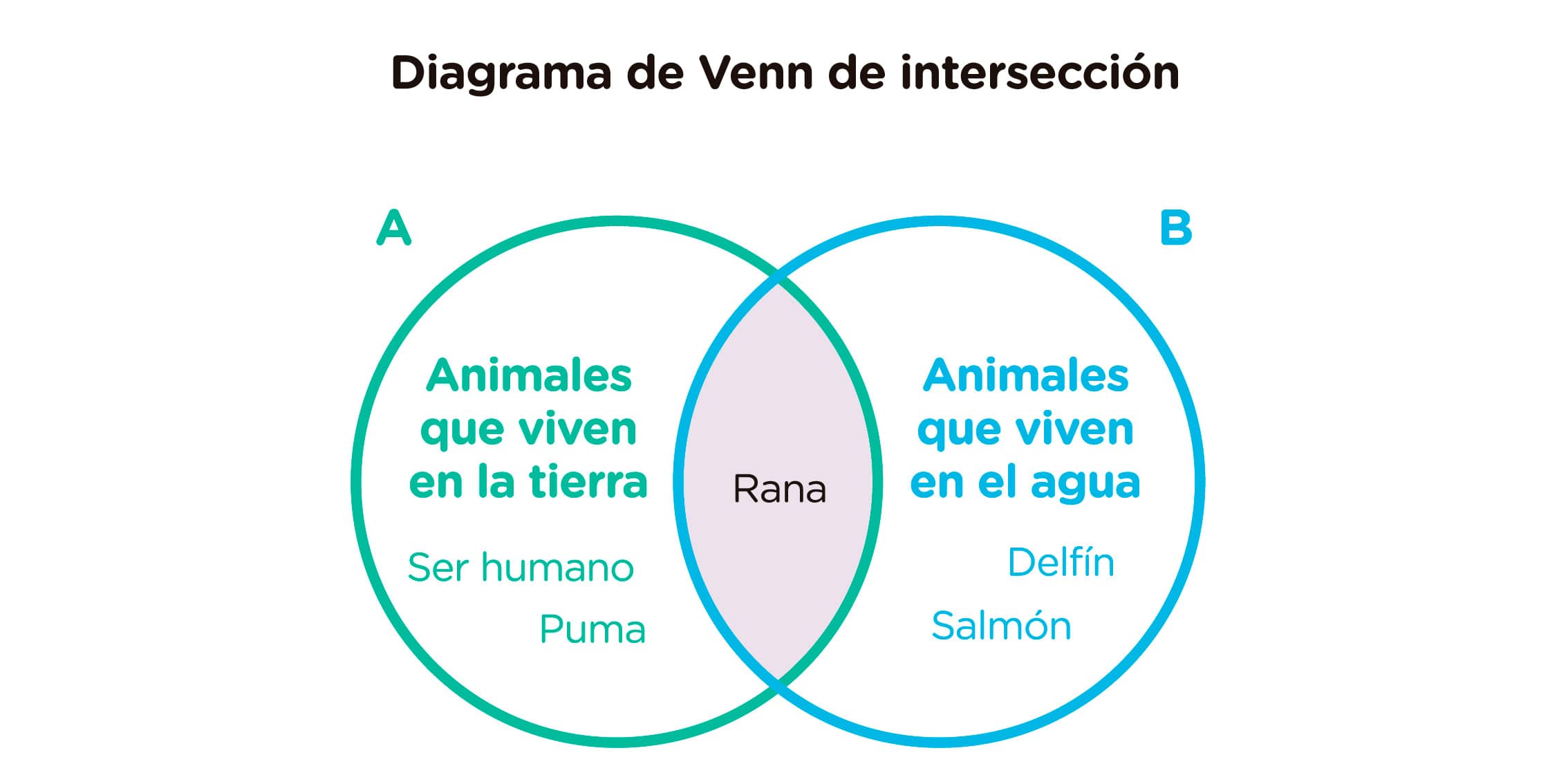
El elemento rana está en la intersección, porque es un animal que vive tanto en la tierra como en el agua.

Diagrama de Venn de inclusión

Muestra que un conjunto incluye a un subconjunto. Por ejemplo:

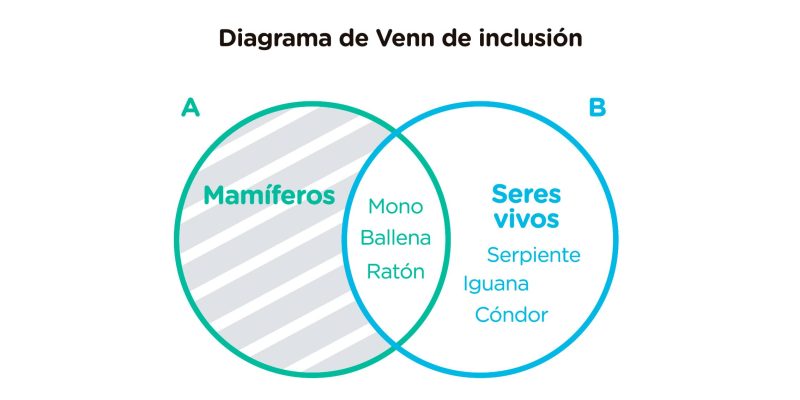
El conjunto B (seres vivos) incluye al subconjunto A (mamíferos), y, como no existen mamíferos que no sean seres vivos, se sombrea o se tacha la parte del círculo mamíferos que no está incluida en seres vivos. Además, el gráfico señala que existen otros seres vivos que no son mamíferos, como la serpiente, la iguana y el cóndor.

Diagrama de Venn de disyunción

Muestra que los conjuntos contienen elementos que no pertenecen a otros conjuntos. Por ejemplo:

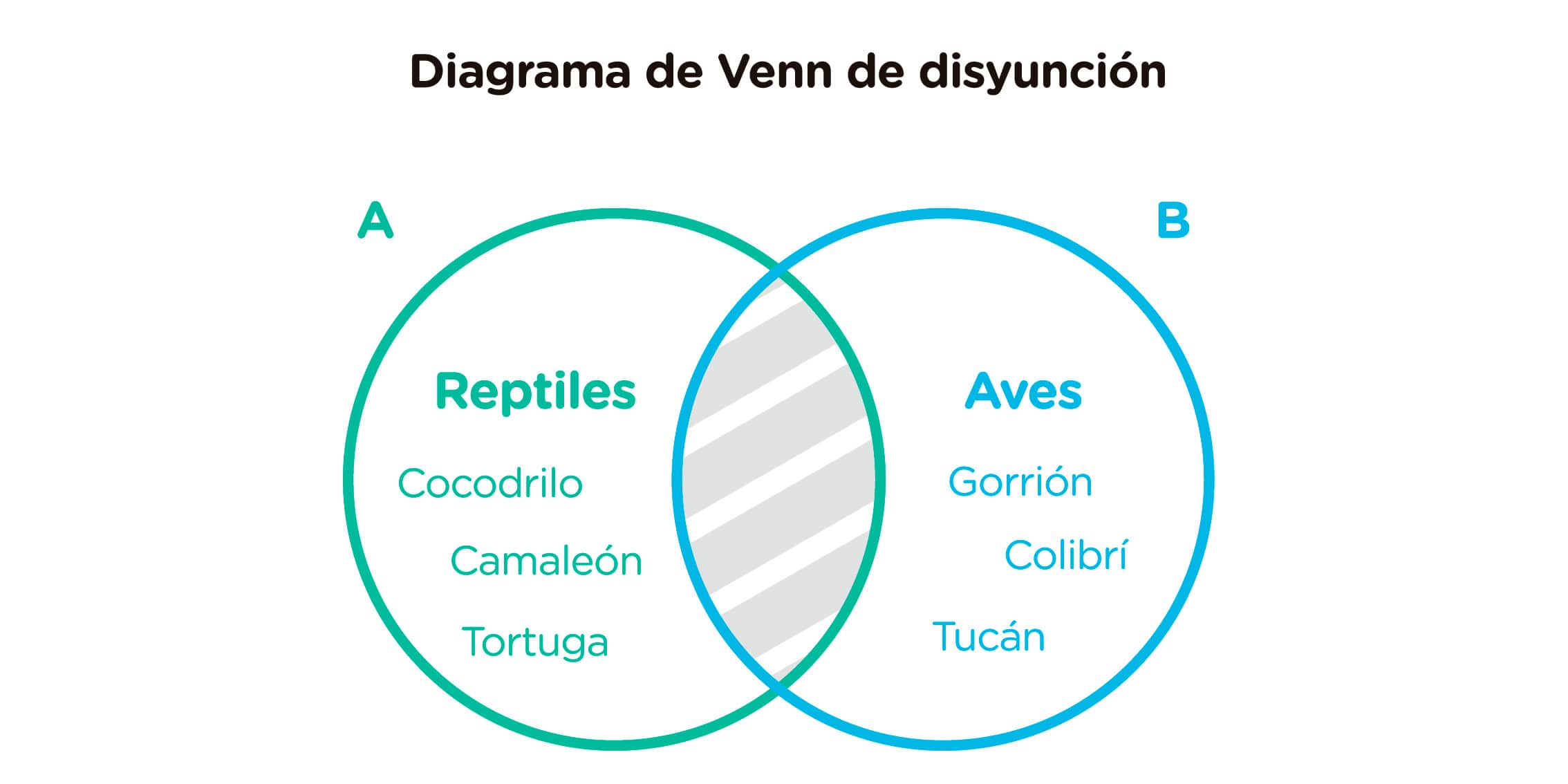
Se sombrea o se tacha la superposición de los círculos, para representar que ningún elemento del conjunto reptiles puede pertenecer al conjunto aves y viceversa.

¿Cómo hacer un diagrama de Venn?

Para hacer un diagrama de Venn, se puede seguir una serie de pasos:

1. Determinar el tema. Se debe seleccionar el tema y qué aspectos se buscan comparar. Por ejemplo, se puede contrastar qué características tienen dos automóviles.
2. Anotar todos los elementos en una lista. Se puede hacer una lluvia de ideas para anotar todos los elementos o las características. Por ejemplo, se pueden escribir todas las características más importantes de los automóviles en general.
3. Determinar los conjuntos. Se debe determinar cuáles son los conjuntos en los que irán los elementos o las características y dibujar un círculo por cada conjunto. Si se comparan dos automóviles, habrá dos círculos superpuestos, uno para el automóvil A y otro para el automóvil B.
4. Indicar qué elemento pertenece a cada conjunto. Se deben anotar los elementos o las características en su conjunto correspondiente. Si algún elemento o característica pertenece a dos conjuntos, se escribe en el sector donde se superponen los círculos. Por ejemplo, la característica “veloz” solo está presente en el automóvil A, entonces se anotará en primer círculo; la característica “confortable” únicamente está presente en el automóvil B, entonces se escribirá en el segundo círculo; y la característica “económico” se encuentra en ambos automóviles, entonces se anotará en la superposición.

Ejemplos del diagrama de Venn

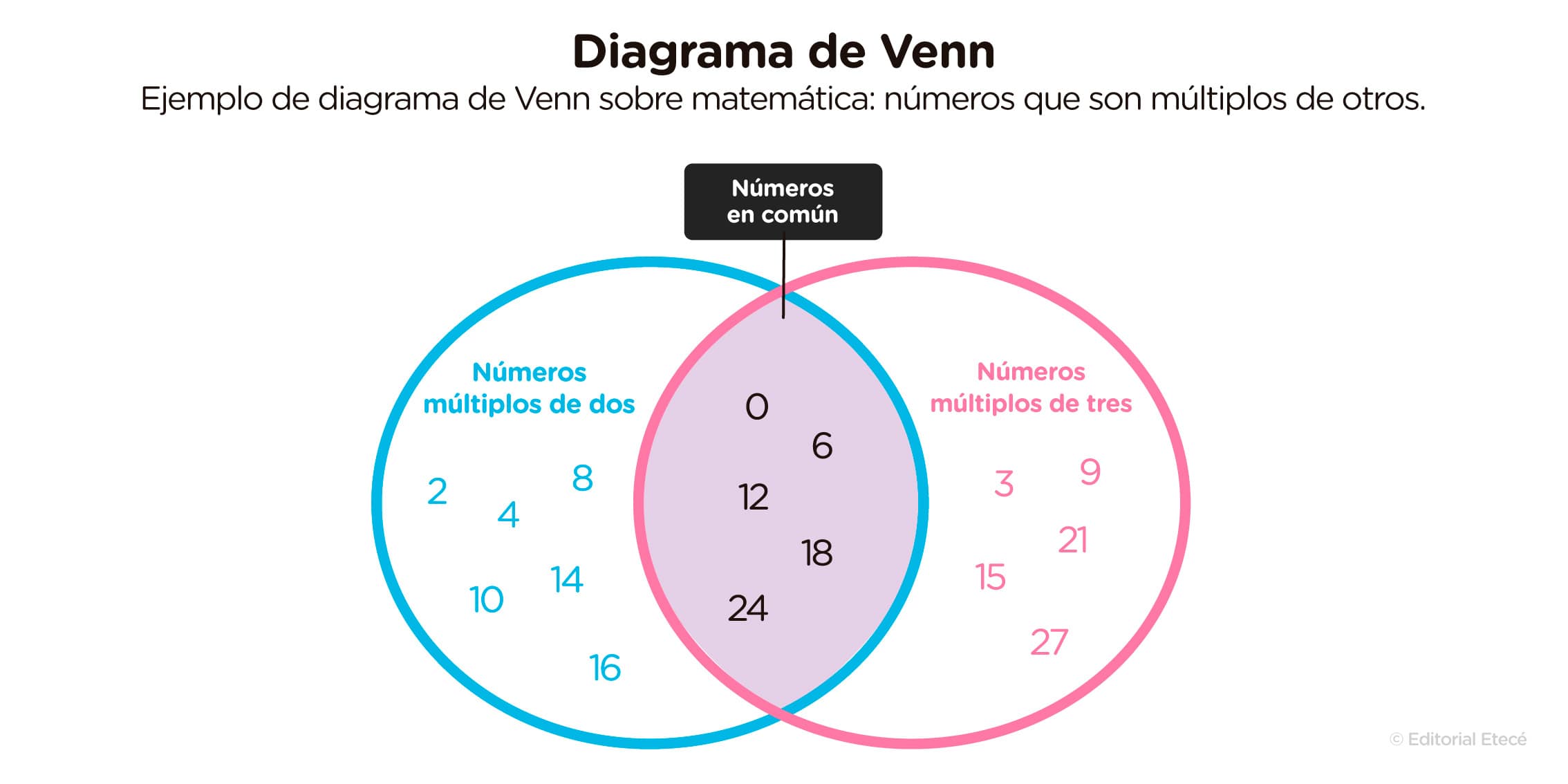
En este diagrama, hay dos conjuntos: números múltiplos de dos y números múltiplos de tres. En cada círculo, se anotan los números correspondientes, y en la superposición, aquellos que son múltiplos de dos y de tres, es decir, que pertenecen a ambos conjuntos.

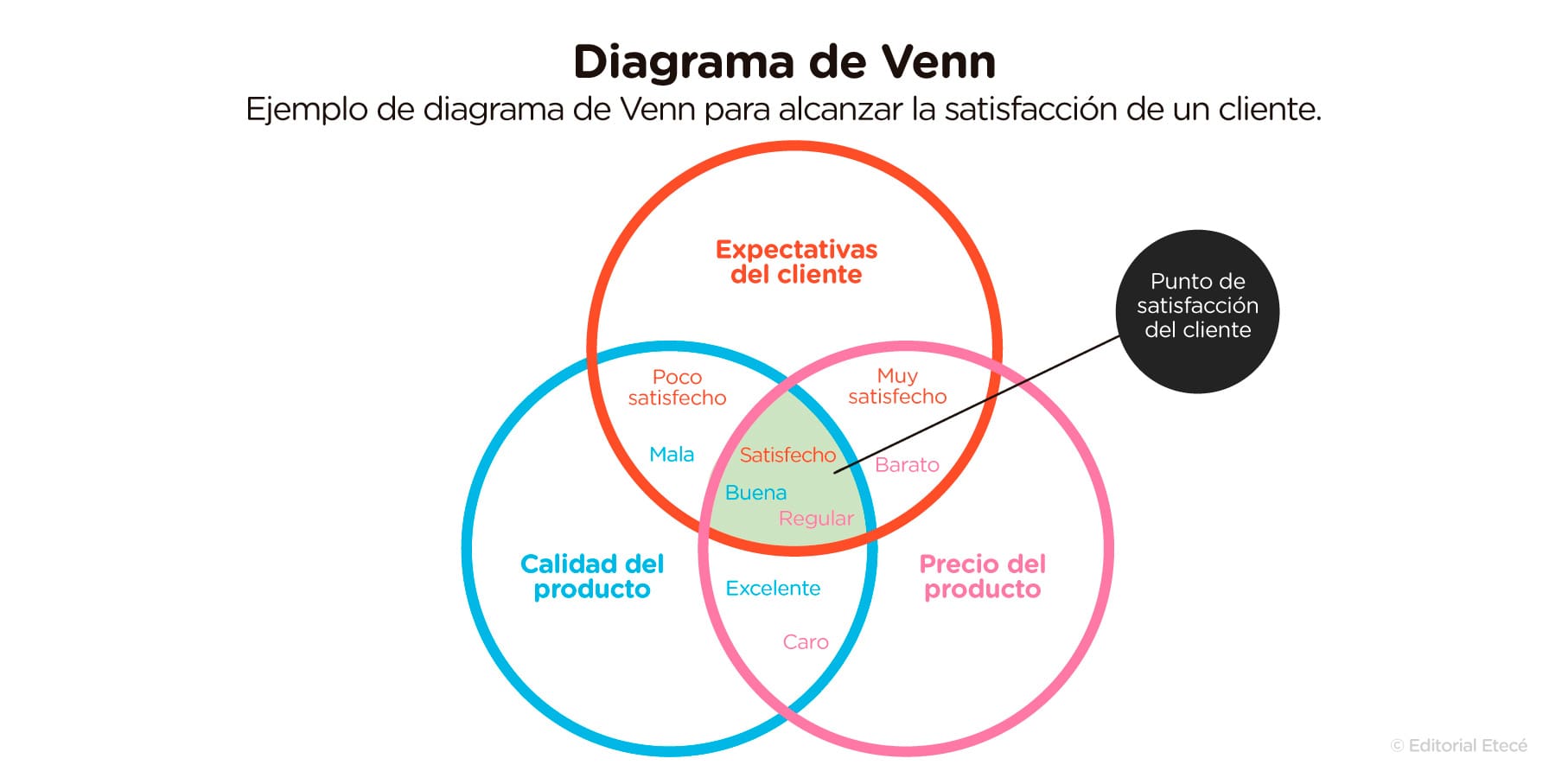
En este diagrama, se mide el punto de satisfacción del cliente que se logra cuando se produce un equilibrio entre las expectativas del cliente, la calidad del producto y el precio del producto.

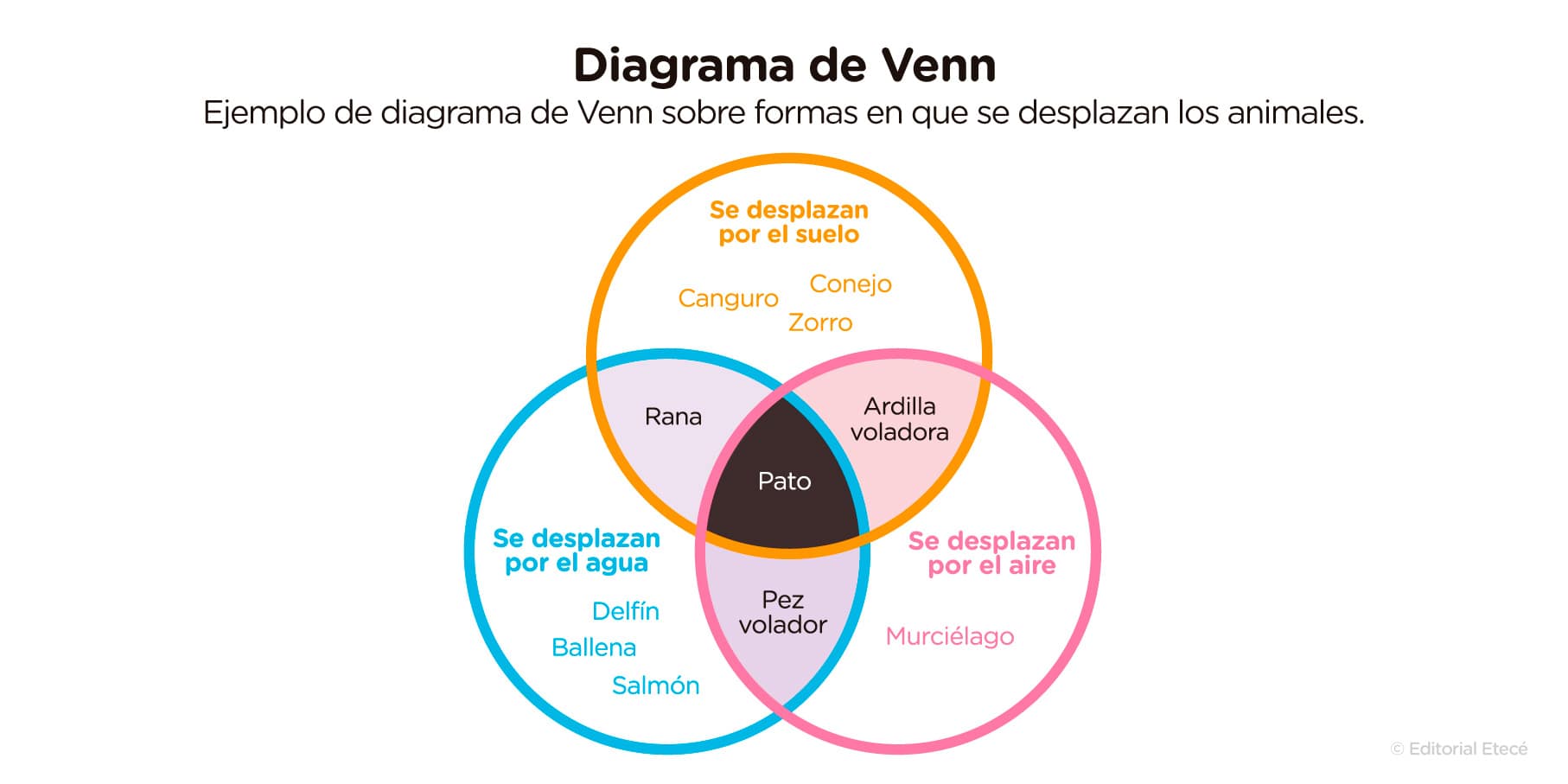
En este diagrama, hay tres conjuntos: animales que se desplazan por el suelo, animales que se desplazan por el agua y animales que se desplazan por el aire. En cada círculo, se anotan los animales que pertenecen a una clase, y en las intersecciones, aquellos que pertenecen a dos o más conjuntos.

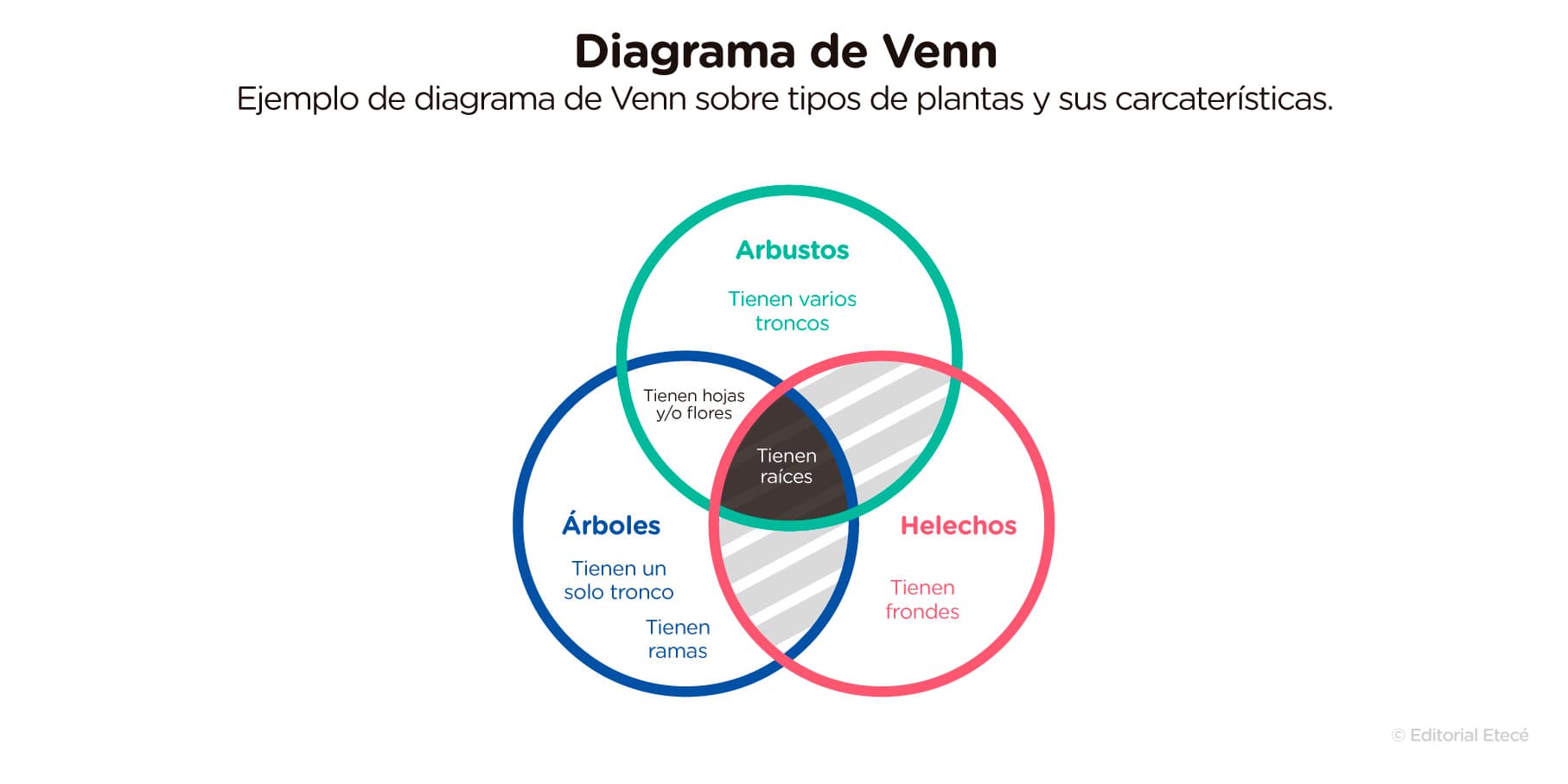
En este diagrama, se mencionan las características de los conjuntos arbustos, árboles y helechos. En las intersecciones, se anotan las características que tienen en común dos o más tipos de plantas. Sin embargo, las superposiciones de arbustos y helechos y de árboles y helechos están tachadas, porque no tienen características en común.

Áreas en que se utiliza el diagrama de Venn

El diagrama de Venn se emplea con distintos objetivos según la disciplina:

• Matemáticas. Sirve para enseñar y aprender de manera didáctica los conjuntos numéricos y sus vínculos. También se aplica en la resolución de ecuaciones y problemas y en análisis probabilísticos.
• Estadística. Sirve para comparar datos cuando se analiza cómo se manifiesta una variable en una población.
• Lógica. Sirve para representar proposiciones y analizar la validez de los argumentos.
• Enseñanza. Sirve para clasificar distintos elementos y para comparar teorías, conceptos y características en diversas asignaturas, como lengua, literatura, ciencias sociales y ciencias naturales.
• Ámbito empresarial. Sirve para analizar y comparar productos, servicios, necesidades de los clientes, procesos productivos, proyectos, entre otros.
• Informática. Sirve para analizar y comparar distintos tipos de datos, como algoritmos y preferencias y búsquedas de usuarios.

Glosario del diagrama de Venn

Los diagramas de Venn se emplean para representar gráficamente los conjuntos y sus operaciones en la teoría de los conjuntos. En esta teoría, se utilizan términos específicos, algunos de los más importantes son:

• Universo. Es aquello que contiene todos los elementos. Por ejemplo, un universo puede estar formado por todos los números que son múltiplos de otros.
• Conjunto. Es aquello que contiene un grupo de elementos que comparten una o más características. Por ejemplo, en un diagrama hay dos conjuntos: números que son múltiplos de 3 y  números que son múltiplos de 4.
• Conjunto vacío. Es un conjunto que no contiene ningún elemento. Por ejemplo, si el universo es todos los libros de una biblioteca y no hay libros de geografía, se sostiene que libros de geografía es un conjunto vacío.
• Elemento. Es un integrante de un conjunto. Por ejemplo, 3, 6 y 9 son elementos del conjunto múltiplos de 3.
• Inclusión. Es el vínculo que indica que un conjunto incluye a un subconjunto. Por ejemplo, el conjunto múltiplos de 9 está incluido en el conjunto múltiplos de 3.
• Pertenencia. Es el vínculo que hay entre un elemento y su conjunto, es decir, que muestra que un elemento pertenece a un conjunto. Por ejemplo, el número 6 pertenece al conjunto múltiplos de 3.
• No pertenencia. Es el vínculo que indica que un elemento no pertenece a un conjunto. Por ejemplo, el número 8 no pertenece al conjunto múltiplos de 3.
• Unión. Es la formación de un nuevo conjunto que se produce cuando todos los elementos de un conjunto pertenecen al de otro y viceversa. Por ejemplo, los conjuntos libros de filosofía y libros de literatura se unen para formar el conjunto libros de humanidades.
• Intersección. Es el grupo de elementos que tienen características de dos o más conjuntos diferentes. Por ejemplo, los números 12, 24, 36 están en la  intersección, porque pertenecen a los conjuntos múltiplos de 3 y  múltiplos de 4.
• Diferencia. Es el grupo de elementos que forman parte de un conjunto, pero no de otro. Por ejemplo,  los números 3, 6 y 9 pertenecen al conjunto múltiplos de 3, pero no al conjunto múltiplos de 4.
• Complemento. Es el grupo de elementos que no pertenecen a un conjunto. Por ejemplo, los números 1, 2 y 4 no forman parte del conjunto múltiplos de 3.

Historia del diagrama de Venn

El diagrama de Venn surgió en 1881, con la publicación de Symbolic Logic, de John Venn, un matemático y lógico británico. En ese libro, el autor desarrolló los distintos tipos de gráficos que se conocen en el presente, pero aplicados a la representación de proposiciones que se utilizaban en álgebra.

Los gráficos inventados por Venn tienen varios antecedentes, pero los más destacados fueron los diseñados por Leonhard Euler, un físico y matemático suizo. Venn simplificó los esquemas Euler, puesto que propuso un solo diagrama que con pequeñas modificaciones pudiera representar todas las proposiciones.

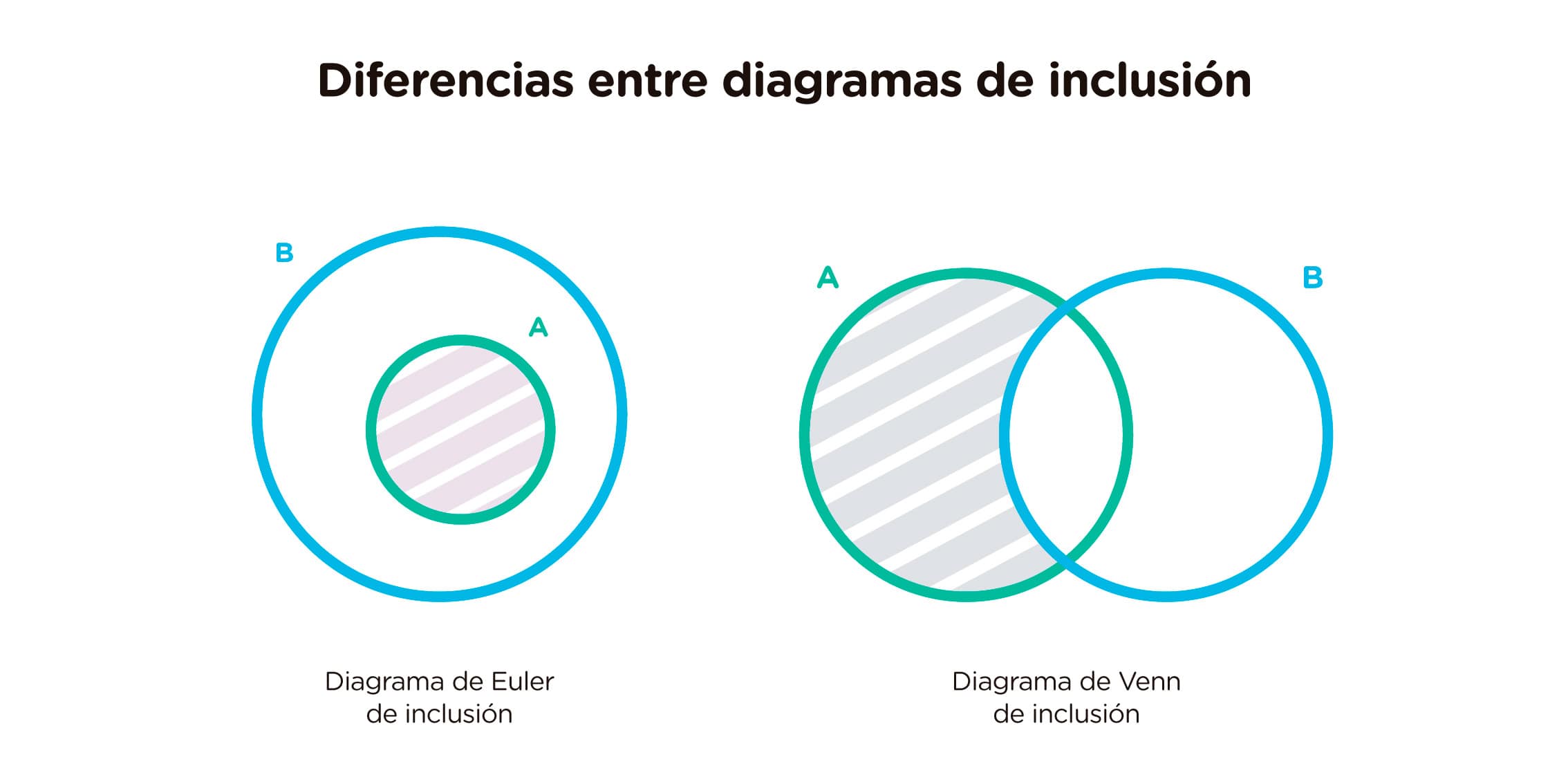
Las principales diferencias entre el diagrama de Venn y el de Euler son:

• El diagrama de Euler que representa la inclusión o la proposición “Todo A es B” consiste en dibujar el círculo del conjunto A dentro del círculo del conjunto B. En cambio, en el diagrama de Venn, se dibujan dos círculos superpuestos y se tacha la parte del conjunto A que no está incluida en el conjunto B.

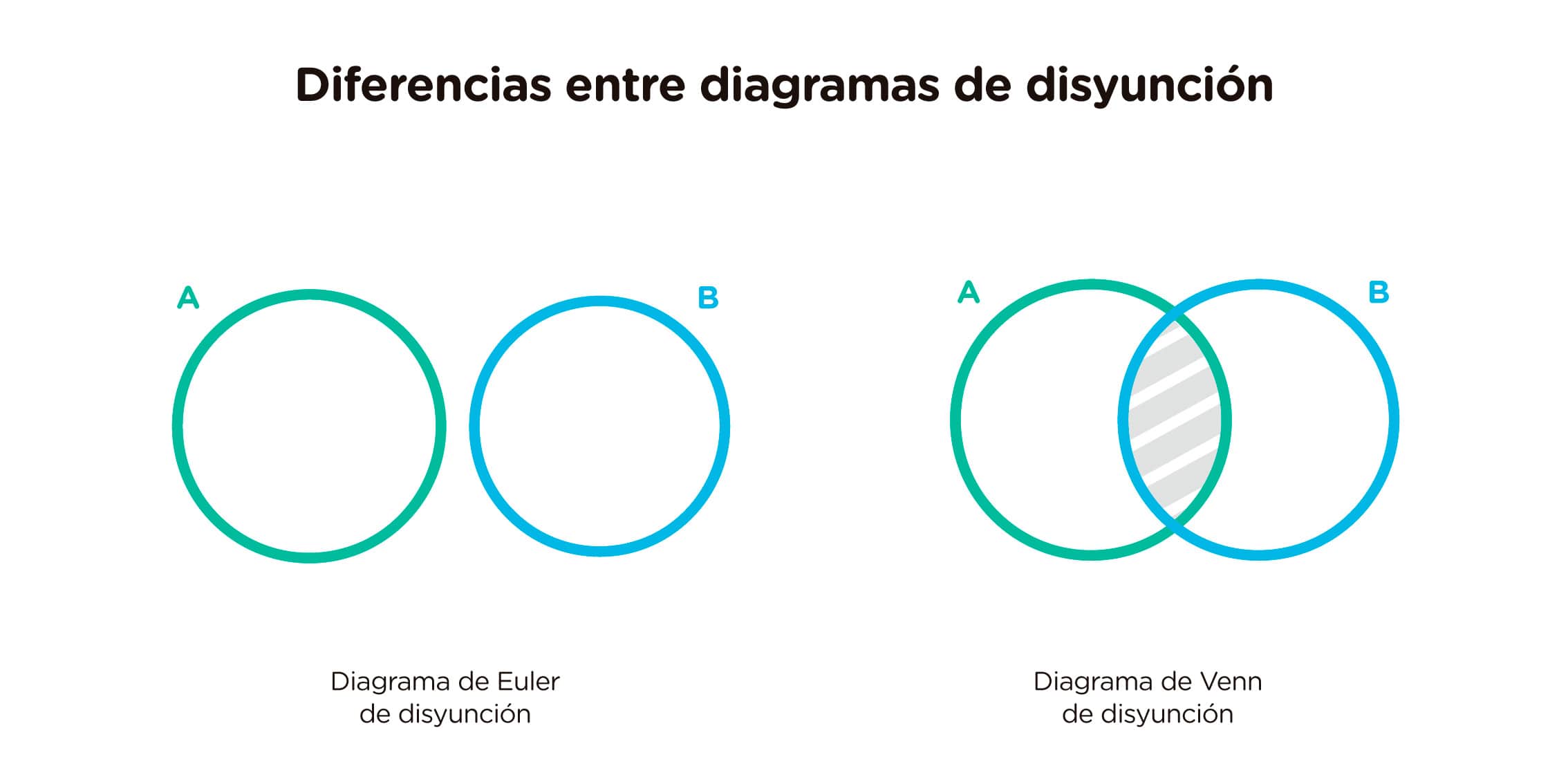
• El diagrama de Euler que representa la disyunción o la proposición “Ningún A es B” consiste en dos círculos separados. En cambio, en el diagrama de Venn, se tacha la superposición de los círculos, para que quede anulada.

• Sigue con: Diagrama de flujo

Referencias

• Canela Morales, L. A. y Ruiz Sosa, F. G. (2019). Aspectos generales del conocimiento simbólico y diagramático: el caso de los diagramas de Venn. Andamios, 16(41), 63-85. https://doi.org/
• Copi, I. M. y Cohen, C. (2013). Introducción a la lógica. Limusa.
• Lipschutz, S. (1991). Teoría de los conjuntos y temas afines. McGraw-Hill.
• Ramírez, F. (2014). Cognotécnicas: Herramientas para pensar más y mejor. Alfaomega.