Te explicamos qué es un polígono de frecuencias en estadística, para qué sirve y cómo hacerlo a partir de un histograma y de Excel.
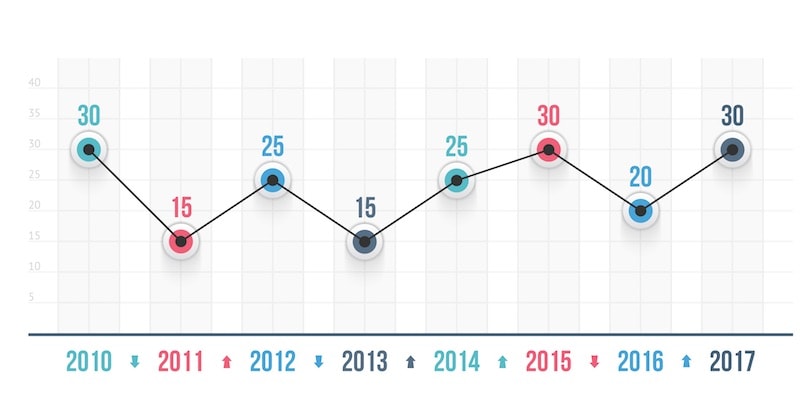
¿Qué es un polígono de frecuencias?
Un polígono de frecuencias es una herramienta gráfica que se emplea a partir de un histograma de frecuencia (es decir, otro tipo de gráfico que expresa las frecuencias mediante columnas verticales). Para ello, se unen con una línea los distintos puntos medios de las columnas del histograma, sin dejar espacio entre una y otra, logrando así una forma geométrica o polígono.
Con esta herramienta gráfica pueden representarse variables cuantitativas o distribuciones diferentes, cosa que tradicionalmente no hace un histograma, de un modo rápido y sencillo. Además cuenta con la virtud de ser apreciable a simple vista.
Por esta razón es sumamente empleado dentro de las ciencias sociales y ciencias económicas, permitiendo así establecer comparaciones útiles entre los distintos resultados de un mismo proceso.
Puede servirte: Método cuantitativo
Características del polígono de frecuencias
Los polígonos de frecuencia se conforman uniendo los puntos medios de cada fase o columna mediante segmentos de recta, de modo que consisten en un tipo de representación visual de la información cuantitativa. Los datos de la tabla se hallan siempre por debajo de la curvatura del polígono, y su punto más alto es siempre el de mayor frecuencia del conjunto.
¿Para qué sirve un polígono de frecuencias?
Se emplean los polígonos de frecuencias cuando es necesario graficar o resaltar distintas distribuciones conjuntas o bien una clasificación cruzada de una variable cuantitativa continua, junto con otra variable cualitativa o cuantitativa discreta, todo dentro de un mismo gráfico.
¿Cómo hacer un polígono de frecuencias?
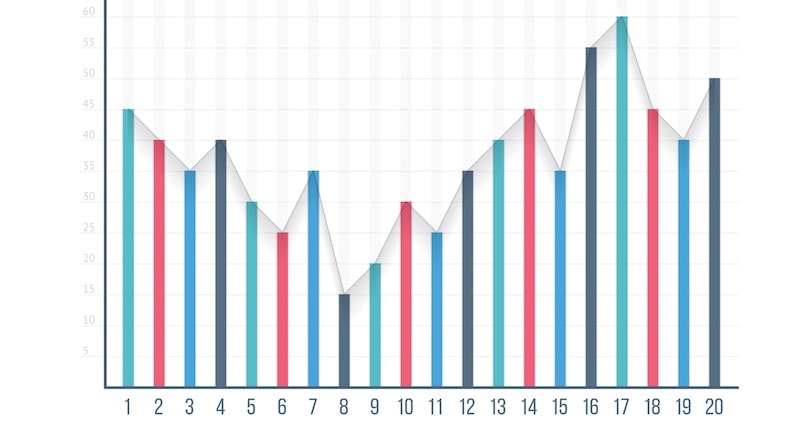
Como hemos dicho ya, se obtiene un polígono de frecuencias siempre a partir de un histograma de frecuencia, cuando se unen consecuentemente todos los puntos medios de cada elemento con su respectiva frecuencia. Para ello se deben seguir los siguientes pasos:
- Recolectar la información cuantitativa de lo que se estudiará. Después se establecerán los límites inferiores y superiores de todos los elementos estudiados.
- Determinar la frecuencia de cada tipo de elemento dentro de los límites establecidos, y se hará el cálculo promedio de los límites.
- Trazar el gráfico lineal cerrado, juntando los puntos medios de los datos obtenidos.
Ejemplos de polígonos de frecuencias
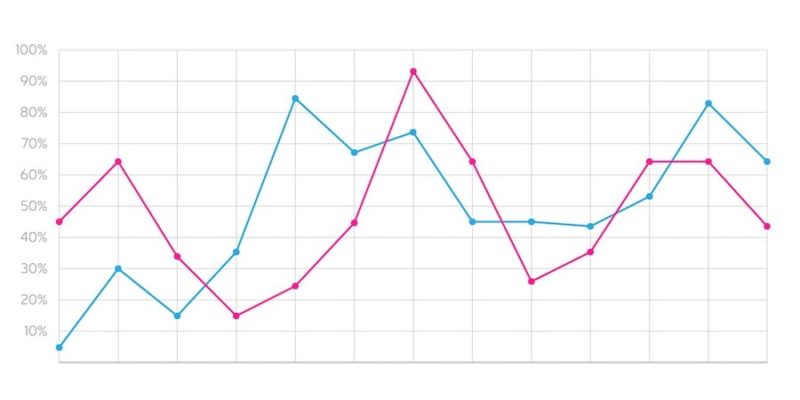

Polígono de frecuencias en Excel
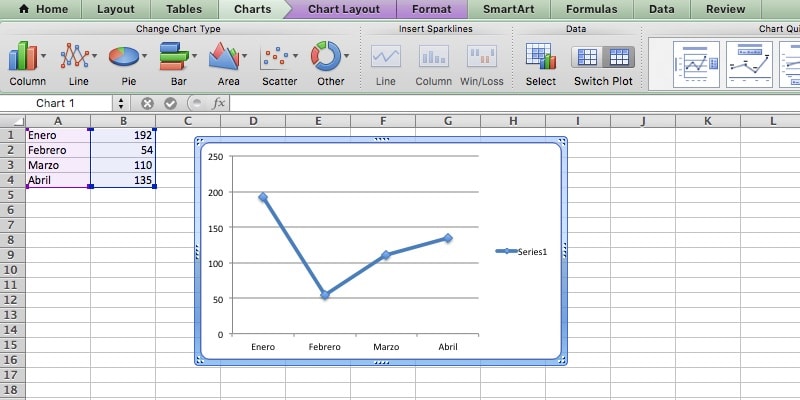
Para realizar un polígono de frecuencias empleando la herramienta informática de Microsoft Excel, debemos seguir los siguientes pasos:
- Obtener primero el cuadro de datos a partir del cual se desea graficar un polígono de frecuencias.
- Buscar el menú “insertar”, y elegir las opciones “gráfico”, luego “línea” y finalmente “línea con marcadores”.
- Aparecerá un recuadro en blanco.
- En el recuadro, en el rango del gráfico, colocar los datos de la columna de frecuencia.
- En el mismo recuadro, en el eje horizontal, elegir la opción de “editar” para colocar la media.
- Presionar “aceptar” para obtener así la gráfica. Recordemos que debe ser un gráfico cerrado, así que a menudo deberemos añadir datos para los intervalos nuevos (en ese caso añadiremos el número 0 a cada uno).
Sigue con: Estadística inferencial
Referencias
- “Histograma” en Wikipedia.
- “Polígono de frecuencias” (video) en Didactikós.
- “Polígonos de frecuencia” en Superprof.
- “Polígono de frecuencias” en Cálculo CC.
- “Histograma y polígono de frecuencias en Excel” en SaberProgramas
¿Te fue útil esta información?
Sí No¡Genial! Gracias por visitarnos :)