Perímetro

Te explicamos qué es un perímetro, cómo se calcula en diferentes figuras geométricas y sus aplicaciones en otras disciplinas.

¿Qué es el perímetro?

En geometría, el perímetro es la suma de las longitudes de los lados de cualquier figura geométrica plana. Se trata de un concepto clave para las matemáticas, que junto con el de área, que le resulta cercano, es necesario dominar para poder transitar hacia matemáticas más avanzadas como el álgebra y la trigonometría, ya que permiten la construcción de polígonos.

La palabra perímetro proviene del griego antiguo (unión de las voces peri, “todo”, y métron, “medida”), ya que los antiguos filósofos griegos fueron los primeros en calcularlo. Se le atribuye el primer pensamiento de este tipo al filósofo Arquímedes (c. 287-212 a. C.).

El concepto aplica tanto para la distancia como la longitud, o para el contorno de las figuras; pero en el caso de los círculos pasa a llamarse circunferencia. La mitad del perímetro se denomina semiperímetro. El perímetro se representa mediante la letra P.

Puede servirte: Pensamiento matemático

Aplicaciones prácticas del perímetro

El cálculo del perímetro posee numerosas aplicaciones prácticas, especialmente para las labores de arquitectura, ingeniería y construcción. Por ejemplo, puede usarse para calcular los bordes o la frontera de un espacio o un objeto, como un terreno o una construcción.

Si deseamos, por ejemplo, colocar una cerca alrededor de nuestro jardín, será necesario calcular el perímetro de su superficie, para saber cuántos materiales comprar y de qué manera colocarlos.

Perímetro de un círculo

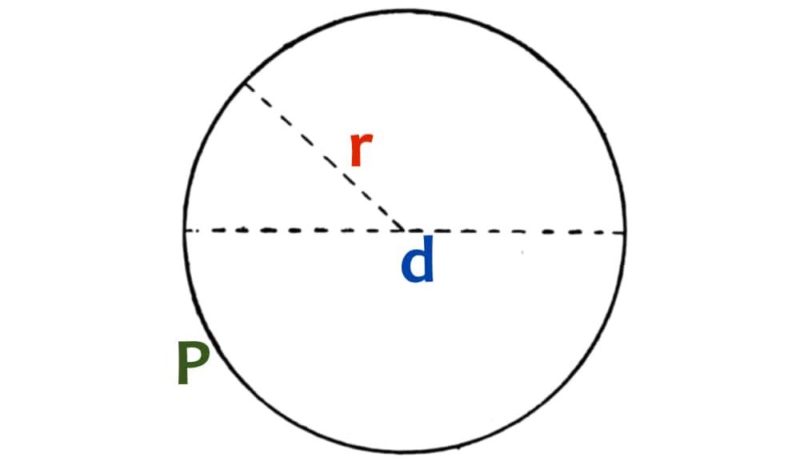
El perímetro de un círculo se llama circunferencia, y se calcula mediante la aplicación de la siguiente fórmula:

P = 2π . r = dπ

Donde π es la constante matemática equivalente a 3,14159…, r es la longitud del radio del círculo y d es la longitud del diámetro del mismo. En el caso de un semicírculo, la fórmula cambiará a:

P = 2r + r . π = r(2 + π)

Perímetro de un rectángulo

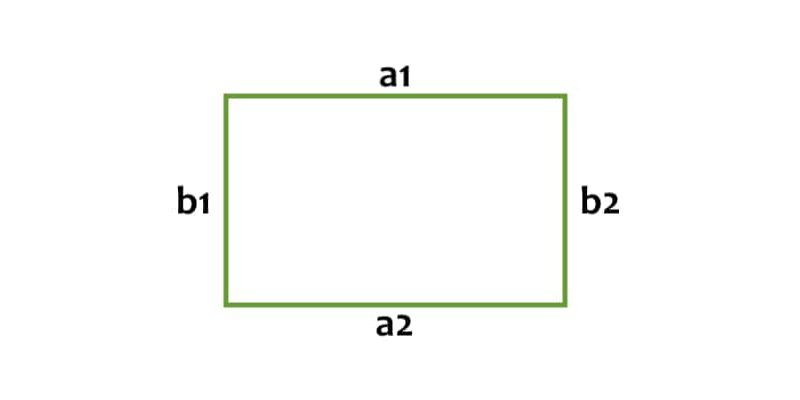
En el caso de un rectángulo, no hará falta para calcular el perímetro más que sumar las longitudes de sus dos lados largos y sus dos lados cortos. Es decir, si el rectángulo tiene dos lados a (a1, a2) y dos lados b (b1, b2), el perímetro se calculará sumando a1 + a2 + b1 + b2.

Perímetro de un cuadrado

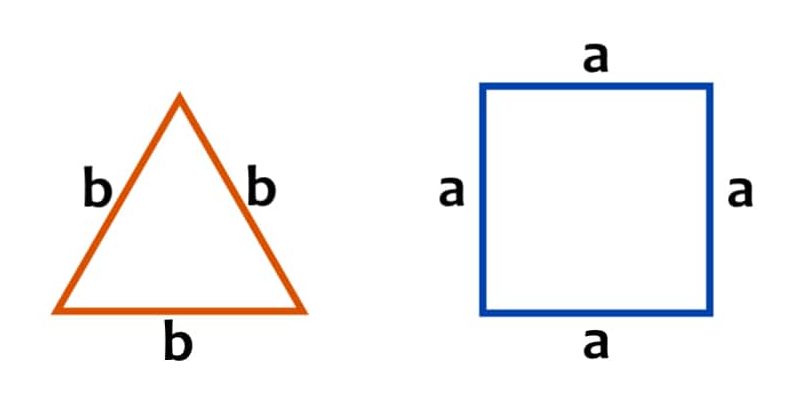
El caso de los cuadrados es idéntico al de los rectángulos. De hecho, en el caso de los polígonos regulares, cuyos lados miden exactamente lo mismo (como los triángulos equiláteros), bastará con multiplicar la longitud de un lado por el número de lados de la figura:

• Cuadrado. 4 lados idénticos que miden a, por lo tanto, P = a x 4.
• Triángulo equilátero. 3 lados idénticos que miden b, por lo tanto, P = b x 3.

Lo mismo aplica para otras figuras semejantes, sin importar su número de lados. En cambio, para los triángulos isósceles y escalenos se deberá sumar cada longitud de cada lado.

Perímetro de un polígono irregular

En el caso de los polígonos irregulares, o sea, de los que no tienen lados y ángulos idénticos, bastará con sumar las medidas de todos los lados del polígono, sin importar su forma. En caso de que no poseamos las medidas de algunos de dichos lados, la labor se complicará pues deberemos primero calcularlos, pero luego podremos proceder a sumarlos sin dificultad alguna.

Sigue con: Poliedros

Referencias

• “Perímetro” en Wikipedia.
• “¿Qué son los perímetros y las áreas?” (video) en Aula365.
• “Perímetro y área” en Monterrey Institute.
• “Calculating the área and perimeter” en Math Planet.
• “Introduction to perimeter” (video) en Khan Academy.