Te explicamos qué es la ley de Hooke, su fórmula y sus aplicaciones en la ingeniería y la arquitectura. Además, cómo se calcula la elasticidad.
¿Qué es la ley de Hooke?
La Ley de elasticidad de Hooke, o simplemente Ley de Hooke, es el principio físico en torno a la conducta elástica de los sólidos. Fue formulada en 1660 por el científico británico Robert Hooke, contemporáneo del célebre Isaac Newton.
El precepto teórico de esta ley es que el desplazamiento o la deformación sufrida por un objeto sometido a una fuerza, será directamente proporcional a la fuerza deformante o a la carga. Es decir, a mayor fuerza, mayor deformación o desplazamiento, o como lo formuló en latín el propio Hooke: Ut tensio sic vis (“como la extensión, así la fuerza”).
La Ley de Hooke es sumamente importante en diversos campos, como en la física y el estudio de resortes elásticos (su demostración más frecuente). Es un concepto fundamental para la ingeniería y la arquitectura, la construcción y el diseño, ya que permite prever la manera en que una fuerza prolongada o un peso alterará las dimensiones de los objetos en el tiempo.
Se dice que esta ley fue publicada por Hooke bajo la forma de un misterioso anagrama (ceiiinosssttuv), del cual puede reconstruirse el enunciado en latín de su ley, porque tenía miedo de que alguien pudiera adueñarse ilegalmente de su descubrimiento. Un par de años más tarde, sin embargo, hizo públicos sus hallazgos.
- Ver además: Propiedades generales de la materia
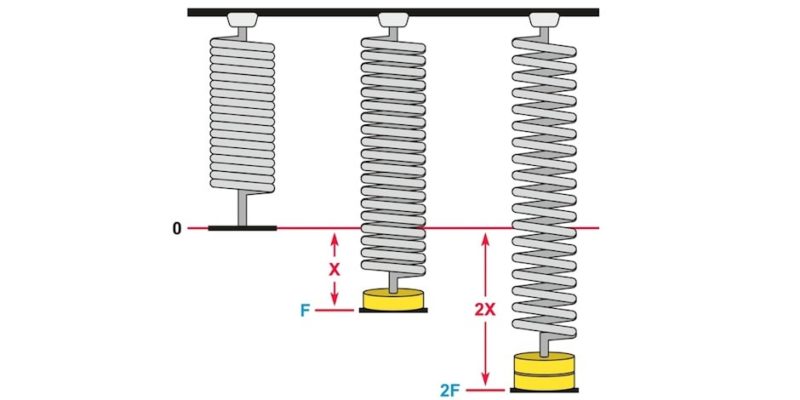
Fórmula de la ley de Hooke para resortes
La fórmula más común de la ley de Hooke es la siguiente:
F = -k . ΔL
Donde:
- F es la fuerza deformante
- ΔL es la variación que experimenta la longitud del resorte, ya sea una compresión o extensión.
- k es la constante de proporcionalidad bautizada como constante de resorte, generalmente expresada en Newtons sobre metros (N/m).
Para el cálculo de ΔL, es decir, la deformación del objeto, es necesario conocer la longitud inicial (L0) y la final (Lf).
- Ver además: Elasticidad en física
Aplicaciones de la ley de Hooke

La ley de Hooke es sumamente útil en todos aquellos campos en los que se requiere del conocimiento pleno de la capacidad elástica de los materiales. La ingeniería, la arquitectura y la construcción son las disciplinas en las que es usada más frecuentemente.
Por ejemplo, esta ley permite predecir el efecto que el peso de los automóviles tendrá sobre un puente y sobre los materiales de los que está hecho (como el metal). También permite calcular el comportamiento de un fuelle o un conjunto de resortes, dentro de alguna máquina específica o aparato industrial.
La aplicación más conocida de la ley de Hooke es la elaboración de los dinamómetros: aparatos compuestos por un resorte y una escala que permiten medir escalarmente fuerzas.
Ley de Hooke y elasticidad
La aplicación de la ley de Hooke para el cálculo de la elasticidad varía si se trata de resortes, o de sólidos elásticos.
Para calcular la elasticidad de los resortes se aplica la “ecuación del muelle”, que es la forma más general de plantear la fórmula de la ley de Hooke (la misma que ofrecimos arriba: F = -k . ΔL).
Conociendo la constante del resorte k y la masa del objeto conectado al resorte, se puede calcular la frecuencia angular de oscilación del resorte (ω), con la siguiente fórmula:
ω = √k/m
En cambio, para calcular la elasticidad de los sólidos elásticos, se deberá generalizar la ley de los resortes, dado que la distribución de la tensión en sus cuerpos es mucho más complicada que un fuelle.
Para eso, se recurre a las ecuaciones de Lamé-Hooke, que poseen fórmulas específicas para cada sólido según su forma específica: unidimensional, tridimensional isótropo o tridimensional ortótropo. Pero estos son temas que requieren una elaboración mucho más compleja y técnica.
Sigue con:
Referencias
- “¿Qué es la Ley de Hooke?” en Khan Academy.
- “Introducción a la ley de Hooke” (video) en Flipping Physics.
- “Hooke’s Law” en Lumen Learning.
- “Hooke’s Law” en The Encyclopaedia Britannica.





¿Te fue útil esta información?
Sí No¡Genial! Gracias por visitarnos :)