Te explicamos qué es la Ley de gravitación universal, cómo es su fórmula y su enunciado. Además, ejemplos del uso de su fórmula.
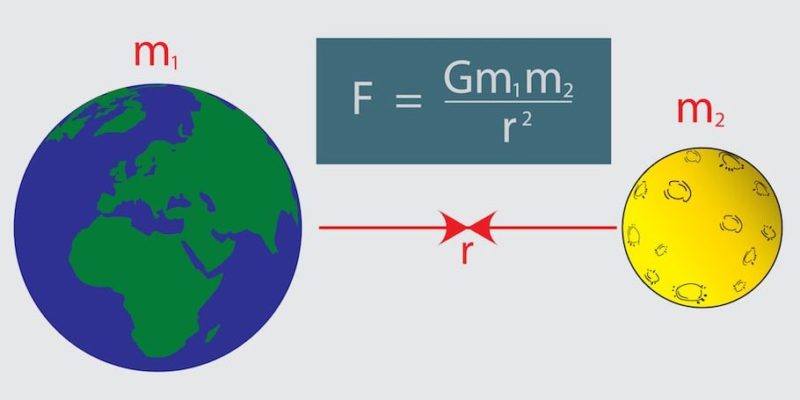
¿Qué es la Ley de gravitación universal?
La Ley de Gravitación Universal es una de las leyes físicas formuladas por Isaac Newton en su libro Philosophiae Naturalis Principia Mathematica de 1687. Describe la interacción gravitatoria entre cuerpos masivos, y establece una relación de proporcionalidad de la fuerza gravitatoria con la masa de los cuerpos.
Para formular esta ley, Newton dedujo que la fuerza con que dos masas se atraen es proporcional al producto de sus masas dividido por la distancia que las separa al cuadrado. Estas deducciones son el resultado de la comprobación empírica mediante la observación.
La ley implica que mientras más cerca y más masivos sean dos cuerpos, más intensamente se atraerán. Como otras leyes newtonianas, representó un salto adelante en el conocimiento científico de la época.
Sin embargo, hoy en día sabemos que, a partir de cierta cantidad de masa, esta ley pierde su validez (en caso de objetos supermasivos), y se hace necesario trabajar con la Ley de Relatividad General formulada en 1915 por Albert Einstein. La Ley de Gravitación Universal es entonces una aproximación a la ley de Einstein pero aun así es útil para comprender la mayor parte de los fenómenos gravitatorios del Sistema Solar.
- Ver además: Campo gravitatorio
Enunciado de la Ley de gravitación universal
El enunciado formal de esta ley newtoniana sostiene que:
“La fuerza con que se atraen dos objetos es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa”.
Esto significa que dos cuerpos cualquiera se atraen con una fuerza mayor o menor según su masa sea mayor o menor, y según la distancia entre ellos.
Fórmula de la Ley de gravitación universal
La fórmula fundamental de la Ley de Gravitación Universal es la siguiente:
F = | (G . m1 . m2) / r² | . r*
En donde:
- F es la fuerza de atracción entre dos masas
- G es la constante de gravitación universal ( 6,673484.10-11 N.m2/kg2)
- m1 es la masa de uno de los cuerpos
- m2 es la masa de otro de los cuerpos
- r la distancia que los separa.
- r* es el vector unidad que indica la dirección de la fuerza.
Si se calculan las fuerzas atractivas de cada cuerpo (la fuerza que la masa 1 le hace a la 2 y viceversa), se tendrán dos fuerzas iguales en módulo y de sentido opuesto. Para obtener esta diferencia de signos, es necesario escribir la ecuación de la siguiente manera:
F12 = | G . m1.m2 / (r11-r2)3 | . (r1-r2)
Donde cambiando 1 por 2 obtenemos la fuerza para cada caso. Escrita de esta forma, el vector (r1-r2) da la dirección (el signo) correcto para cada fuerza.
Ejemplos de la Ley de gravitación universal
Resolvamos un par de ejercicios como ejemplo de la aplicación de esta fórmula.
- Supongamos que una masa de 800 kg y otra de 500 kg se atraen en el vacío, separadas por un espacio de 3 metros. ¿Cómo podemos calcular la fuerza de atracción que experimentan?
Simplemente aplicando la fórmula:
F = G. (m1.m2)/r2
Que será: F = (6.67×10-11 N.m2/kg2) . (800 kg . 500 kg) / (3m)2
Y luego: F = 2.964 x 10-6 N. - Otro ejercicio: ¿A qué distancia debemos colocar dos cuerpos de masa de 1 kg, para que se atraigan con una fuerza de 1 N?
Partiendo de la misma fórmula:
F = G. (m1.m2)/r2
Despejaremos la distancia, quedándonos que r2 = G.(m1.m2)/ F
O lo que es lo mismo: r = √(G.[m1.m2])/ F
Es decir: r = √(6.67×10-11 N.m2/kg2 . 1kg x 1kg) / 1N
El resultado es que r = 8.16 x 10-6 metros.
Sigue con:
Referencias
- “Ley de Gravitación Universal” en FísicaLab.
- “Ley de Gravitación Universal” (video) en Profesor Particular Puebla.
- “Isaac Newton y la ley de la gravitación universal” AstroMía.
- “Newton’s Law of Gravitation” en The Encyclopaedia Britannica.



¿Te fue útil esta información?
Sí No¡Genial! Gracias por visitarnos :)