Te explicamos qué son los lenguajes formales, sus características, ejemplos y tipos. Además, sus diferencias con los lenguajes naturales.

¿Qué es un lenguaje formal?
Un lenguaje formal es un lenguaje artificial que, a diferencia de los lenguajes naturales, no está centrado en la comunicación humana habitual, sino en la definición y aplicación de una serie de reglas específicas en un entorno específico. Consta de una serie de símbolos básicos, que se combinan en cadenas para formar expresiones complejas.
Los símbolos constituyen el alfabeto de un lenguaje formal, mientras que las cadenas son las palabras. Tanto la combinación de los símbolos como la interpretación de las cadenas se realiza de acuerdo con reglas rigurosas, establecidas de antemano, que no admiten excepciones; en conjunto, estas reglas conforman la gramática del lenguaje.
Frente a la creatividad y complejidad del lenguaje natural, que permiten su uso en las más diversas situaciones, los lenguajes formales han sido diseñados para ser utilizados en contextos muy precisos. Su campo de aplicación incluye la lógica, las matemáticas, la informática y la lingüística.
No se deben confundir los lenguajes formales aquí tratados con el registro lingüístico formal (también llamado a veces lenguaje formal), correspondiente al uso cuidadoso y correcto del lenguaje, propio de ciertas situaciones comunicativas, opuesto al registro informal, en el que se emplean frases y expresiones coloquiales.
Ver también: Tipos de lenguaje
Tipos de lenguajes formales
En un artículo publicado en 1956, el lingüista estadounidense Noam Chomsky (1928-) estableció cuatro tipos de lenguajes formales, en función de las gramáticas que los generan. En el contexto de un lenguaje formal, se entiende por gramática al conjunto de reglas para formar cadenas de símbolos correctas.
Para comprender la clasificación de Chomsky –al menos en sus aspectos más generales– debe tenerse en cuenta que una gramática formal está integrada por cuatro componentes:
- Símbolos terminales (∑). Comprenden los elementos básicos del lenguaje (el alfabeto).
- Símbolos no terminales (N). Denominados a veces “variables sintácticas”, son de carácter auxiliar; expresan estados intermedios en el proceso de generación de las palabras. No forman parte del lenguaje.
- Símbolo inicial o axioma (S ∈ N). Es un símbolo no terminal de inicio, del que se parte para la formación de cualquiera de las palabras del lenguaje.
- Conjunto de reglas de producción (P). Son reglas que, partiendo del símbolo inicial, permiten realizar las transformaciones necesarias para obtener las palabras del lenguaje, mediante el reemplazo de los símbolos no terminales por símbolos terminales.
Los cuatro tipos de lenguajes formales descriptos por Chomsky son los siguientes:
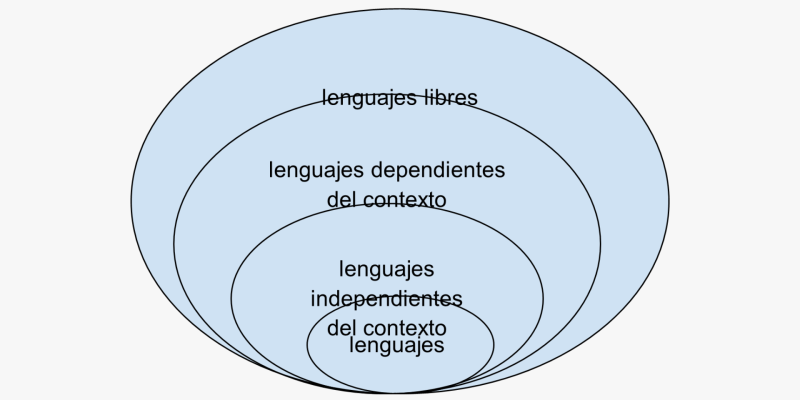
- Tipo 3: lenguajes regulares o lineales. Aquellos generados por gramáticas regulares. Sus cadenas se caracterizan por contener dependencias lineales. Esto significa que la posición de un símbolo en una cadena depende únicamente del símbolo que lo precede. La calificación de regulares dada a este tipo de lenguajes obedece al hecho de que sus cadenas contienen regularidades o repeticiones de los mismos símbolos.
- Tipo 2: lenguajes independientes del contexto. Aquellos que pueden ser reconocidos por una gramática libre de contexto. Las producciones de las gramáticas que dan lugar a estos lenguajes se atienen a la regla que establece que un símbolo no terminal puede ser siempre reemplazado por una cadena de símbolos no terminales o terminales sin considerar el contexto en el que se encuentre. Este tipo de lenguajes son los que más desarrollo han tenido, debido a que son la base de la mayoría de los lenguajes de programación.
- Tipo 1: lenguajes dependientes del contexto. Aquellos definidos por gramáticas dependientes del contexto. Se reconocen porque permiten el reemplazo de símbolos no terminales solo en ciertos contextos. Las producciones de las gramáticas que generan estos lenguajes se caracterizan por poseer un único símbolo no terminal del lado izquierdo; su lado derecho puede estar compuesto por un símbolo terminal y un símbolo no terminal. Se trata del tipo de lenguajes que poseen producciones más restringidas.
- Tipo 0: lenguajes libres o recursivamente enumerables. Responden a gramáticas libres. Las producciones pueden contener cadenas de terminales y no terminales tanto en el lado derecho como en el lado izquierdo.
Entre los cuatro tipos de lenguajes existe una relación jerárquica, en la que cada tipo incluye a otros, de manera tal que los lenguajes de menor numeración abarcan a los de mayor numeración, como se muestra en el siguiente esquema:
Aplicaciones de los lenguajes formales
Las principales aplicaciones de los lenguajes formales son en el campo de la informática, la lógica y la matemática.
- En informática, los lenguajes formales constituyen la base para la definición de los lenguajes de programación.
- En lógica simbólica (también llamada lógica formal), se emplean lenguajes formales para expresar de manera clara y simple las proposiciones y razonamientos, a fin de determinar su validez.
- En matemática, los lenguajes formales se emplean para representar relaciones, operaciones y fórmulas.
- En lingüística, los lenguajes formales son estudiados en sus aspectos sintácticos, con el fin de comprender las regularidades de las lenguas naturales.
Ejemplos de lenguajes formales
Son ejemplos de lenguajes formales:
- Informática. El siguiente es un ejemplo de cadena de caracteres del lenguaje de programación C.char str[12]= “bienvenidos”;donde char es la variable de caracteres y str de cadena. La cadena de caracteres es bienvenidos.
- Lógica. Las siguientes combinaciones de símbolos expresan tipos de enunciados: p∧q significa “p y q”, donde p y q son dos proposiciones.
∽ (r ∧ p) → q
significa “si r y p, entonces q”, donde r, p y q son proposiciones. - Matemática. El teorema de Pitágoras afirma que “en todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos”. Esta afirmación se puede expresar matemáticamente mediante la siguiente ecuación:
a2 + b2 = c2
donde a y b son la medida de los catetos y c la medida de la hipotenusa
Sigue con: Lenguaje técnico
Referencias
- “Lenguaje formal”, en https://es.wikipedia.org/
- “Jerarquía de Chomsky” en https://es.wikipedia.org/
- Teoría de los lenguajes formales. Una introducción para lingüistas, de Sergio Balari, en la Universidad Autónoma de Barcelona (España). https://ddd.uab.cat/
- “Lenguajes formales”, por Federico Peinado, en la Universidad Complutense de Madrid (España). http://www.fdi.ucm.es/
- “Formal language”, en https://www.britannica.com/
¿Te fue útil esta información?
Sí No¡Genial! Gracias por visitarnos :)