Te explicamos qué es un porcentaje, para qué sirve, cómo se expresa y cómo se calcula. Además, te ofrecemos diversos ejemplos prácticos.

¿Qué es un porcentaje?
En matemáticas y estadística, un porcentaje es la expresión de una cantidad como una fracción de cien (100) partes iguales. En otras palabras, el porcentaje representa la relación de proporcionalidad entre dos magnitudes o entre una parte y un total, expresada como un número por cada 100 unidades (literalmente: tanto por cada ciento o cada centena).
El porcentaje se expresa con el signo %, que acompaña a la cifra. Por ejemplo: 25 % (un cuarto), 50 % (la mitad) o 100 % (el total). De este modo, el porcentaje permite expresar cuánto representa una cantidad respecto a otra o del conjunto total.
Por ejemplo, si en una bolsa hay cien manzanas, ese total representa el 100 % de las manzanas (100 de cada 100). Si se regalan cincuenta manzanas, quedará el 50 % de las manzanas iniciales, es decir, la mitad. Y si de esas cincuenta resultan dañadas veinticinco, se conservará únicamente el 25 % del total inicial, equivalente a un cuarto del total.
Los porcentajes son muy útiles para comparar proporciones o expresar la relación entre partes de un conjunto. Por eso, se emplean con frecuencia en disciplinas como la estadística, la demografía y la ecología. Su uso en Occidente se remonta al siglo XV, como una herramienta para calcular los impuestos que correspondían a la corona, ya que es más sencillo operar con porcentajes que con cifras fraccionarias.
Entonces:
- 1 / 1 equivale a 100 / 100, es decir, 100 % del total
- 1 / 10 equivale a 10 / 100, es decir, 10 % del total
- 1 / 200 equivale a 0,5 / 100, es decir, 0,5 % del total
Y siguiendo la misma lógica:
- ½ equivale al 50 % (la mitad del total)
- ¼ equivale al 25 % (la cuarta parte del total)
- ⅔ equivale al 66,6 % (dos terceras partes del total)
Sin embargo, los porcentajes pueden expresarse en cifras enteras o decimales, y es posible realizar operaciones aritméticas entre ellas, siempre que se recuerde que un porcentaje no expresa una cifra absoluta, sino una proporción. Por lo tanto, si el valor de referencia aumenta o disminuye, el porcentaje correspondiente también se modificará.
Por ejemplo, retomando el caso de las manzanas: si inicialmente había cien manzanas y se regalaron cincuenta (50 %), pero luego se compran cien más, el total asciende a doscientas manzanas, y las cincuenta regaladas ya no representan el 50 %, sino el 25 % del nuevo total.
Ver además: Incidencia
¿Cómo calcular un porcentaje?
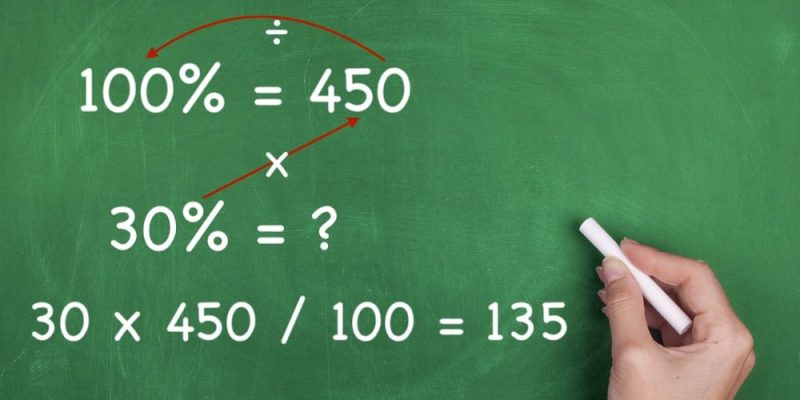
Para calcular el porcentaje de un número, se debe multiplicar la cifra por el porcentaje deseado y dividirlo el resultado entre 100.
Por ejemplo, si queremos saber cuánto es el 30 % de 450, multipliquemos 30 x 450 y dividimos el resultado entre 100. El resultado final es 135, de modo que el 30 % de 450 es 135.
Otra forma de resolverlo es aplicando una regla de tres simple:
Si el 100 % equivale a 450,
entonces el 30% equivale a X
Para despejar la incógnita (X), multiplicamos en diagonal (30 x 450) y dividimos entre 100. La ecuación queda de la siguiente manera:
X = (30 x 450) / 100
x = 13.500 / 100
X = 135
Ejemplos prácticos de porcentajes
A continuación se detallan algunos ejemplos prácticos de aplicación del cálculo de porcentajes:
- Un trabajador desea saber cuánto le descuentan de impuestos de su salario. En su empresa le informan que se le retiene el 15 % mensual. Si su salario es de 1500 pesos, ¿cuánto le quitan de impuesto mensualmente y cuánto cobra en realidad?
Cálculo:
(15 x 1500) / 100 = 225 pesos se le descuenta de impuestos.
1500 – 225 = 1275 pesos es lo que cobra en realidad.
- Otro empleado de la misma empresa cobra 2200 pesos, pero recibe solo 1870 pesos después de impuestos. ¿Cuánto le descuentan y qué porcentaje de su salario representa esa retención?
Cálculo:
2200 – 1870 = 330 pesos se le retienen o descuentan de impuestos.
(330 x 100) / 2200 = 15 % de su salario es lo que se le retiene para impuestos.
Entonces, se confirma que la retención equivale al mismo porcentaje que la del primer trabajador.
- Al mes siguiente, la empresa anuncia un aumento general del 7 %. Los dos trabajadores desean calcular cuánto aumentará su sueldo y cuánto pagarán en impuestos después del ajuste.
Dado que el aumento será porcentual (7 %), la cifra exacta variará dependiendo del salario de cada trabajador.
Primer trabajador (salario 2200 pesos):
Aumento: (7 x 2200) / 100 = 154 pesos.
Nuevo salario: 2200 + 154 = 2354 pesos.
Impuesto del 15 %: (15 x 2354) / 100 = 353 pesos.
Salario neto tras impuestos: 2354 – 353,10 = 2000,90 pesos.
Segundo trabajador (salario 1500 pesos):
Aumento: (7 x 1500) / 100 = 105 pesos.
Nuevo salario: 1500 + 105 = 1605 pesos.
Impuesto del 15 %: (15 x 1605) / 100 = 240,75 pesos.
Salario neto tras impuestos: 1605 – 240,75 = 1364,25 pesos.
Sigue con:
Referencias
- “Cómo sacar el porcentaje de un número” en https://www.clarin.com/
- “Finding a percent” (video) en https://www.khanacademy.org/
- “Porcentaje” en https://www.britannica.com/




¿Te fue útil esta información?
Sí No¡Genial! Gracias por visitarnos :)