Te explicamos qué es un teorema, su función y cuáles son sus partes. Además, los teoremas de Pitágoras, de Tales, de Bayes y otros.

¿Qué es un teorema?
Un teorema es una proposición que, partiendo de ciertas suposiciones o hipótesis, puede afirmar de manera comprobable una tesis no evidente por sí misma (pues en ese caso sería un axioma). Son muy frecuentes dentro de los lenguajes formales, como las matemáticas o la lógica, ya que en ellos constituyen la enunciación de ciertas reglas formales o reglas “de juego”.
Los teoremas no solo proponen relaciones estables entre las premisas y la conclusión, sino que también brindan las claves fundamentales para comprobarlo. La demostración de teoremas es, de hecho, una parte clave de la lógica matemática, pues de un teorema pueden derivarse otros y así agrandar el conocimiento del sistema formal.
Sin embargo, en el campo de los estudios matemáticos, se usa el término “teorema” solo para las proposiciones de particular interés entre la comunidad académica. En cambio, en la lógica de primer orden cualquier afirmación demostrable constituye en sí misma un teorema.
La palabra “teorema” proviene del griego theórema, derivado del verbo theorein, que significa “contemplar”, “juzgar” o “reflexionar”, de donde proviene también la palabra “teoría”.
Para los antiguos griegos, un teorema era el resultado de una observación y reflexión detenida y atenta, y fue un término que emplearon con mucha frecuencia numerosos filósofos y matemáticos de la época. De allí proviene también la distinción académica entre los términos “teorema” y “problema”: el primero es de tipo teórico y el segundo de tipo práctico.
Todo teorema consta de tres partes:
- Hipótesis o premisas. Es el contenido lógico a partir del cual se puede deducir la conclusión y que, por lo tanto, la antecede.
- Tesis o conclusión. Es aquello que se afirma en el teorema y que se puede demostrar formalmente a partir de lo propuesto por las premisas.
- Corolarios. Son aquellas deducciones o formulaciones secundarias y adicionales que se obtienen a partir del teorema.
Puede servirte: Pensamiento lógico
Teorema de Pitágoras
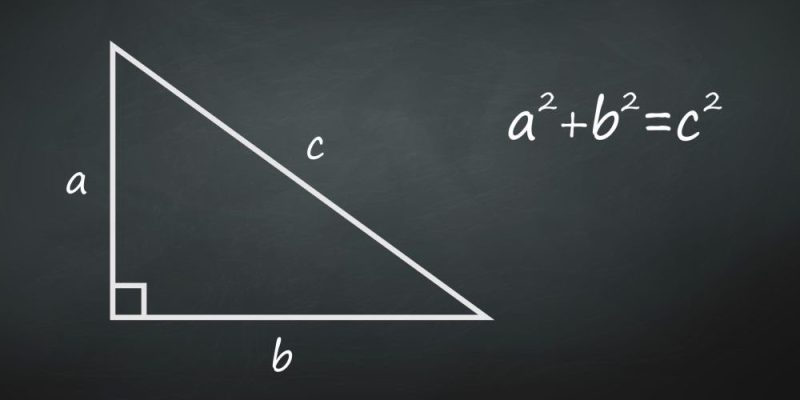
El teorema de Pitágoras es uno de los teoremas matemáticos más antiguos conocidos por la humanidad. Se le atribuye al filósofo griego Pitágoras de Samos (c. 569 – c. 475 a. C.), aunque se cree que el teorema es mucho más antiguo, posiblemente de origen babilonio, y que Pitágoras fue el primero en comprobarlo.
Este teorema propone que, dado un triángulo rectángulo (o sea, que tenga al menos un ángulo recto), el cuadrado de la longitud del lado del triángulo contrario al ángulo recto (la hipotenusa) será siempre igual a la suma del cuadrado de la longitud de los otros dos lados (llamados catetos). Esto se enuncia de la siguiente manera:
En todo triángulo rectángulo, el cuadrado de la hipotenusa será igual a la suma de los cuadrados de los catetos.
Y con la siguiente fórmula:
a2 + b2 = c2
Donde a y b equivalen a la longitud de los catetos y c a la longitud de la hipotenusa. De allí también pueden deducirse tres corolarios, es decir, fórmulas derivadas que tienen aplicación práctica y verificación algebraica:
a = √c2 – b2
b = √c2 – a2
c = √a2 + b2
El teorema de Pitágoras ha sido demostrado numerosas veces a lo largo de la historia: por el propio Pitágoras y por otros geómetras y matemáticos como Euclides, Pappus, Bhaskara, Leonardo da Vinci, Garfield, entre otros.
Teorema de Tales
Atribuido al matemático griego Tales de Mileto (c. 624 – c. 546 a. C.), este teorema en dos partes (o bien estos dos teoremas con el mismo nombre) tiene que ver con la geometría de los triángulos, de la siguiente manera:
- El primer teorema de Tales propone que si uno de los lados de un triángulo es continuado más allá mediante una línea paralela, se obtendrá un triángulo mayor pero de las mismas proporciones. Esto puede expresarse de la siguiente manera:
Dados dos triángulos proporcionales, uno grande y otro pequeño, el cociente de dos de los lados del triángulo grande (A y B) será siempre igual al cociente de los mismos lados del pequeño (C y D).
A/B = C/D
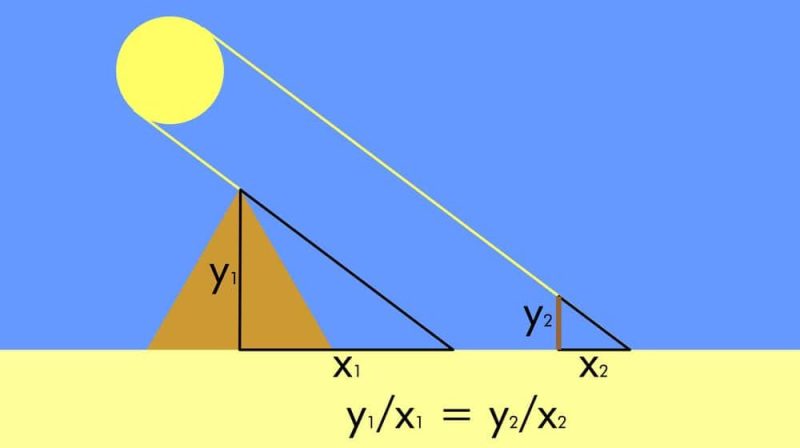
Este teorema sirvió, según el historiador griego Heródoto, a Tales para medir el tamaño de la pirámide de Keops en Egipto, sin tener que utilizar instrumentos de inmenso tamaño.
- El segundo teorema de Tales propone que dada una circunferencia cuyo diámetro sea AC y centro “O” (distinto de A y de C), puede formarse un triángulo rectángulo ABC tal que <ABC = 90°. Esto quiere decir que cualquier triángulo formado a partir del diámetro (AC) de la circunferencia y que tenga su punto B en algún lugar de ella, tendrá necesariamente un ángulo recto.
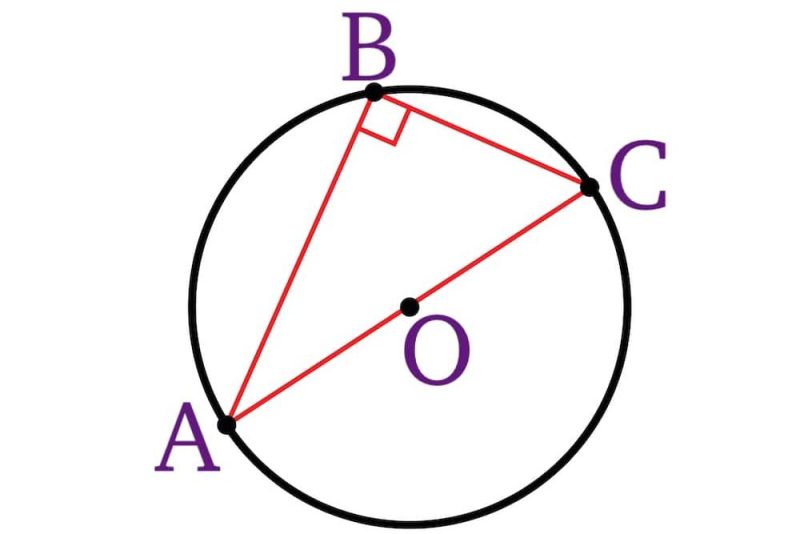
De allí se desprenden dos corolarios:
- En todo triángulo rectángulo, la longitud de la mediana correspondiente a la hipotenusa es siempre la mitad de la hipotenusa.
- La circunferencia circunscrita a todo triángulo rectángulo tiene siempre un radio igual a la mitad de la hipotenusa y su circuncentro se ubicará en el punto medio de la hipotenusa.
Teorema de Bayes
El teorema de Bayes fue planteado por el matemático inglés Thomas Bayes (1702-1761) y publicado luego de su muerte en 1763. Este teorema expresa la probabilidad de que ocurra un evento “A dado B” y su vinculación con la probabilidad de un evento “B dado A”. Este teorema es muy importante en la teoría de la probabilidad, y se formula de la siguiente manera:

Esto quiere decir que es posible calcular la probabilidad de un evento (A) si sabemos que cumple con cierta condición necesaria para que ocurra, de manera inversa al teorema de la probabilidad total.
Otros teoremas conocidos
Otros teoremas célebres son:
- El teorema de Ptolomeo. Sostiene que en todo cuadrilátero cíclico, la suma de los productos de los pares de los lados opuestos es igual al producto de sus diagonales.
- El teorema de Euler-Fermat. Sostiene que si a y n son enteros primos relativos, entonces n divide a aᵩ(n)-1.
- El teorema de Lagrange. Sostiene que si f es una función continua en un intervalo cerrado [a, b] y diferenciable en el intervalo abierto (a, b), entonces existe un punto c en (a, b) de modo que una recta tangente en dicho punto sea paralela a la recta secante que pasa por los puntos (a, f(a)) y (b, f(b)).
- Teorema de Thomas. Sostiene que si las personas establecen una situación como real, dicha situación pasa a ser real en sus consecuencias.
Sigue con: Lenguaje algebraico
Referencias
- “Teorema” en Wikipedia.
- “Etimología de Teorema” en el Diccionario Etimológico Castellano En Línea.
- “Theorem (logic and mathematics)” en The Encyclopaedia Britannica.

¿Te fue útil esta información?
Sí No¡Genial! Gracias por visitarnos :)