Suma

Te explicamos qué es la suma o adición en matemáticas, su historia, propiedades y ejemplos. Además, métodos para la suma de fracciones.

¿Qué es la suma?

La suma o adición es una operación matemática fundamental, que consiste en la incorporación de nuevos elementos a un conjunto numérico, esto es, a la fusión de dos números para obtener uno nuevo, que exprese el valor total de los dos anteriores. La suma es el principio fundamental con el que aprendemos a vincularnos con los números, ya que el mero hecho de contar de a uno en uno (1, 2, 3, 4…) supone sumar 1 (1+0, 1+1, 1+2, 1+3…).

La suma es una operación de tipo aritmético, que permite combinar números de distinto tipo: naturales, enteros, fracciones, reales, racionales, irracionales y complejos, así como estructuras asociadas a ellos, como espacios vectoriales o matrices. En el álgebra moderna se la representa con el símbolo +, intercalado entre los elementos a sumar, y expresado verbalmente como “más”: “1 + 1 = 2” se lee “uno más uno es igual a dos”.

Por otra parte, los elementos que se desea sumar se conocen como “sumandos”, y el número obtenido al final se llama “resultado”.

Puede servirte: Matemáticas

Historia de la suma

La suma es una de las operaciones matemáticas más antiguas y básicas que se conocen. Se piensa que el ser humano del neolítico ya manejaba los principios matemáticos elementales, entre los que necesariamente estarían la adición y la resta, dado que estas operaciones son fáciles de evidenciar de cara a las provisiones agrícolas que aumentaban y disminuían conforme a la época del año.

Sin embargo, el estudio de la suma y su aplicación a tanto números naturales como fraccionarios comenzó con los antiguos egipcios, y continuó desarrollándose en aspectos más complejos con los babilonios, y especialmente con los chinos y los hindúes, quienes fueron los primeros en sumar números negativos. Pero recién en el Renacimiento el auge de la banca impuso la suma de decimales y de logaritmos vulgares.

Propiedades de la suma

La suma en tanto operación matemática posee un conjunto de propiedades, que son:

• Propiedad conmutativa. Establece que el orden de los sumandos no altera el resultado, es decir, que a + b es exactamente lo mismo que b + a, y en ambos casos se obtiene el mismo resultado.
• Propiedad asociativa. Establece que a la hora de sumar tres o más elementos, es posible agrupar dos de ellos para resolverlos primero, independientemente de cuáles sean, sin alterar el resultado final. Es decir, si deseamos sumar a + b +c, podemos optar por dos caminos: (a + b) + c ó a + (b + c), sin afectar en absoluto el resultado.
• Propiedad de identidad. Establece que el cero es un elemento neutro en la operación, de modo que sumarlo con cualquier otro número dará siempre como resultado este mismo último número: a + 0 = a.
• Propiedad clausurativa. Establece que el resultado de una suma pertenecerá siempre al mismo conjunto numérico de los sumandos, siempre que estos a su vez compartan el mismo conjunto. Es decir, si los sumandos a y b pertenecen a N (naturales), Z (enteros), Q (irracionales), R (reales) o C (complejos), el resultado de la suma también pertenecerá al mismo conjunto.

Ejemplos de suma

A continuación algunos ejemplos sencillos de suma:

• Una mujer tiene cuatro flores, pero es su cumpleaños y le regalan ocho más. ¿Cuántas flores tiene al final del día? 4 flores + 8 flores = 12 flores.
• Un pastor tiene 15 ovejas, mientras que un colega suyo tiene 13. Si deciden fusionar sus rebaños, ¿cuántas ovejas tendrán en total? 15 ovejas + 13 ovejas = 28 ovejas.
• Un árbol de manzanas le da a su dueño 5 manzanas al mes. ¿Cuántas manzanas tendrá al término de un año? Como un año son 12 meses, debemos sumar 5 doce veces, aplicando la propiedad asociativa: (5 + 5) + (5 + 5) + (5 + 5) + (5 + 5) + (5 + 5) + (5 + 5) = (10 + 10) + (10 + 10) + (10 + 10) = 20 + 20 + 20 = 60 manzanas en un año.

Suma de fracciones

A la hora de sumar fracciones, existen distintos métodos que podemos aplicar para obtener el resultado, dependiendo de si se trata de fracciones propias, impropias y mixtas.

• Método para sumar fracciones con el mismo denominador. Este es el caso más simple, en el que simplemente sumamos los numeradores y conservamos el mismo denominador. Por ejemplo:

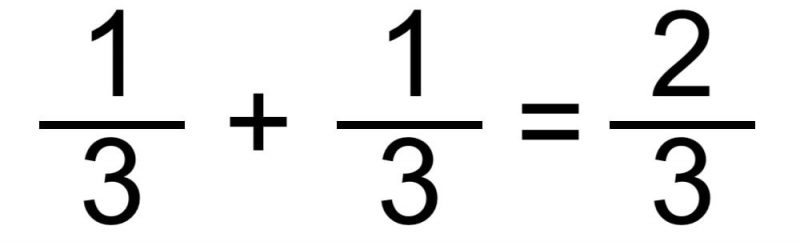
o

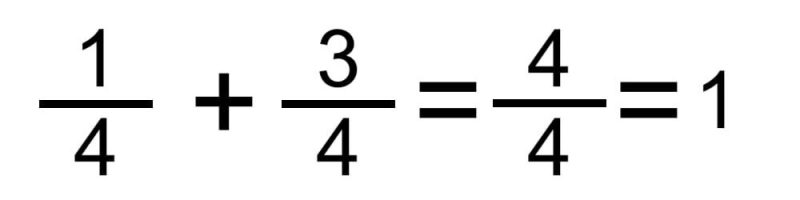
• Método de la mariposa. Este método nos permite sumar cualquier tipo de fracciones de distinto denominador, simplemente multiplicando el numerador de la primera por el denominador de la segunda y viceversa, y luego sumando los productos (para obtener el numerador), y después multiplicando los denominadores para obtener el denominador de la fracción final. Una vez realizadas estas operaciones, a menudo deberemos reducir el resultado. Por ejemplo:

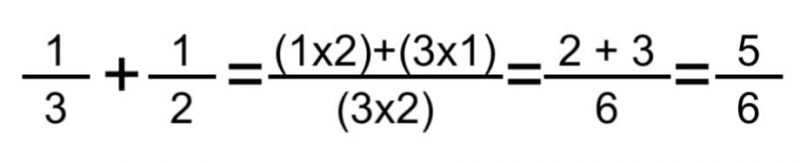
• Método para sumar tres fracciones. En este caso, simplemente sumamos las dos primeras y al resultado le sumamos la última, aplicando el método previo y reduciendo o simplificando el resultado de hacer falta. Por ejemplo:

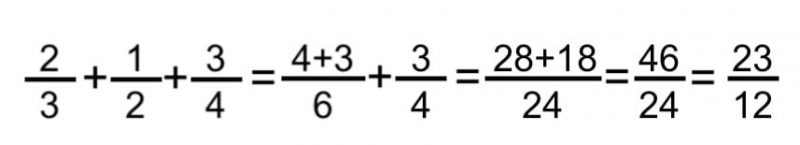
Sigue con: Hoja de cálculo

Referencias

• “Adición” en Wikipedia.
• “Propiedades de la suma” en GCF Global.
• “Propiedades de la suma” en Khan Academy.
• “Suma y resta de fracciones” en Micrositio de Matemáticas para Educación Básica (México).